Physicians in need of help

There is a high incidence of psychiatric problems in the medical community. Physicians may have a difficult time finding help. There are a variety of reasons for this, the most common of which is that the sources of help may all involve people the physician knows personally.

In BC we have something called the "physician health program", which is a resource especially for physicians in need of help. Here is the website:
http://www.physicianhealth.com/

Hopefully other communities have similar programs.

If a hospital admission is needed, it may be desired to arrange this in a different place, if privacy or confidentiality issues are major concerns.

Exercise benefits Quality of Life

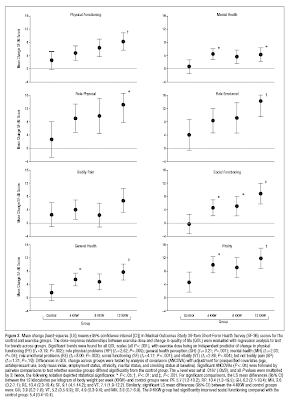
You can click on the chart to expand it; the chart above is from a randomized, controlled, 2009 study by CK Martin et al., published in the major journal Archives of Internal Medicine, in which 6 months of regular aerobic exercise is shown to improve numerous domains of quality of life, including mental health, vitality, and social functioning, in a group of 430 sedentary postmenopausal women.

To interpret the chart, look at each symptom domain. There is a control group (which did not exercise), then groups which exercised approximately 1, 2, and 4 hours per week, with the groups which exercised more represented towards the right-hand side of the chart.

The improvement in quality of life did not depend on any weight loss occurring with the exercise. And it appeared that as little as an hour a week of exercise was beneficial, though 2-4 hours per week were slightly more beneficial than just one. Here's a link to the abstract:

http://www.ncbi.nlm.nih.gov/pubmed/19204218

As a cautionary note, I find "exercise addiction" to be another potentially serious problem, which could substantially REDUCE quality of life. The above data support a very modest amount of exercise, in the order of 4 hours PER WEEK , for improving quality of life.

I strongly encourage people to exercise. I believe it is basic self-care, a requirement for health.

It is intuitively obvious that exercise would be beneficial for psychological health, and be a good potential therapy for depression or anxiety.

Yet, there is an important recent study of over 5000 Dutch twins, which shows that exercise did not have a direct influence on anxiety or depression. This is a surprising result, but it needs to be taken seriously. Twin studies are very powerful in research, since they look at individuals who are genetically identical -- any differences in symptoms would have to be caused by environmental factors, as opposed to genes. Twins who exercised more than their co-twins were not in fact any less anxious or depressed. (Actually, as I look at the results directly, I see there was a small association, but it was judged to be "non-significant")

The study did confirm that people who exercise are, on average, less anxious and depressed than those who do not exercise. But the conclusion was that this is not because exercise improves emotional symptoms -- it is because there is a genetic factor which predisposes some people both to exercise more, and to have fewer psychological symptoms.

Here is a link to the study:
http://www.ncbi.nlm.nih.gov/pubmed/18678794

On the other hand, there are a few studies which show a therapeutic effect of exercise on psychological symptoms:

http://www.ncbi.nlm.nih.gov/pubmed/17846259

http://www.ncbi.nlm.nih.gov/pubmed/11020092

The above studies show a beneficial effect of exercise, of at least 3 times per week, 30 minutes per session.

Why are there seeming contradictions with these studies?

It may be because the twin study was looking at individuals' intrinsic exercise behaviours, as determined by their life circumstances & inherited factors. Variations in exercise between twins may have been due mainly to opportunity or chance.

The other studies were looking at exercise as a formally prescribed treatment. This would involve a directed change of behaviour, outside of what the individuals would normally do on their own.

It could be that prescribed changes of behaviour, if adhered to for health reasons, could have a stronger therapeutic effect than the behaviours engaged in for other reasons.

Active Placebo Studies show smaller benefits from Antidepressants

In most of the better clinical studies, a "placebo group" acts as a control. The placebo would consist of something totally inert, such as a capsule with nothing inside, or possibly with a small quantity of a sugar such as lactose.

The idea of an "active placebo" is interesting: in this case, the placebo is an agent shown not to have any beneficial or detrimental effect on the disease in question, but which clearly has side-effects.

An example would be using a tablet of Gravol (dimenhydrinate) as the "placebo". It is not an antidepressant, but it has side-effects (sedation, dry mouth, etc.). In this way, it is a more convincing placebo, since a person taking an agent which produces side effects is more likely to believe that they are taking the "active" agent. If a person is taking a placebo they strongly believe to be a placebo (since it produces no side effects) they are less likely to have any "placebo effect" response, and the whole point of the placebo control will be relatively "unblinded."

There is a body of research literature looking at using "active placebo" vs. antidepressants to treat depression.

http://www.ncbi.nlm.nih.gov/pubmed/9614471

{a 1998 meta-analysis from the British Journal of Psychiatry showing that the effect sizes of antidepressant therapy are only about half as large when compared against an active placebo, rather than an inert placebo}

http://www.ncbi.nlm.nih.gov/pubmed/14974002
{a 2004 Cochrane review with similar findings}

These results support the evidence that antidepressants work -- but they suggest that probably most of the studies overestimate how well they work, because they are measured against inert placebos in most cases.

I think that more clinical studies need to include active placebos.

I post this not to be cynical, or to discourage the use of antidepressants--as you can see from the rest of this blog, I strongly support medication trials to treat psychiatric problems--but I believe that we have to always search for the most accurate, least biased sources of information. We need to be wary of exaggerated claims about the effectiveness of anything, especially since I see in my practice that many of the treatments don't seem to work quite as well as the ads claim they should.

Trazodone

Trazodone is another antidepressant introduced in the early 80's. Once again, its use was fashionable for a time, gradually faded, and at this point it is mainly used adjunctively to treat insomnia.

It is notable among antidepressant choices in not causing sexual side effects (other than the rare incidence of priapism, which is a medically dangerous, painful, abnormally sustained penile erection, which occurs in probably less than 1 in 1000).

The trouble with trazodone is that for many people, it causes too much daytime sedation. However, it can be worth a try, to treat insomnia associated with depression or antidepressant therapy, or possibly as an augmentation to treat depression or OCD.

In my experience, about 50% of people find trazodone a helpful adjuct, but the other 50% find it causes too much tiredness or dizziness the next day to be worth continuing.

Here is a literature review:


http://www.ncbi.nlm.nih.gov/pubmed/19112384
{in this 2008 study from a minor journal, trazodone was shown to increase the amount of slow-wave sleep in treating chronic insomnia}

http://www.ncbi.nlm.nih.gov/pubmed/12930437
{a 2003 urology article showing evidence that trazodone may help treat erectile dysfunction, especially at higher doses}

http://www.ncbi.nlm.nih.gov/pubmed/18978492
{a small 2008 study showing that 50-100 mg of trazodone may reduce SSRI-induced sexual dysfunction}

http://www.ncbi.nlm.nih.gov/pubmed/16968574
{a small 2006 study showing equivalence between trazodone and sertraline in treating depression over 6 weeks}

http://www.ncbi.nlm.nih.gov/pubmed/10507215
{a small 1999 study from a podiatry journal, showing that trazodone can help with painful diabetic neuropathy symptoms}

http://www.ncbi.nlm.nih.gov/pubmed/8010365
{a 1994 American Journal of Psychiatry article showing that trazodone can help with antidepressant-induced insomnia, particularly helping with overall subjective sleep quality, reducing waking in the middle of the night, and reducing early morning waking}

http://www.ncbi.nlm.nih.gov/pubmed/8988452
{this awkardly-designed 1996 study suggests that combination treatment including 100 mg of trazodone may help in treatment-resistant depression}

http://www.ncbi.nlm.nih.gov/pubmed/11518472
{this quite weak 2001 study nevertheless suggests that trazodone helps to reduce nightmares in PTSD patients}

http://www.ncbi.nlm.nih.gov/pubmed/6337131
{an early, 1983 study, of trazodone vs. imipramine for treating moderately to severely depressed outpatients. Despite the weaknesses of the study design, it did have some follow-up over 3 years, showing that trazodone works well for some people, and worked as well as imipramine overall}

http://www.ncbi.nlm.nih.gov/pubmed/18311107
{an example of a small study suggesting that adjunctive trazodone could help improve OCD symptoms. Some studies have shown no anti-OCD effect with trazodone alone, but others have shown trazodone alone to be beneficial in refractory OCD. In any case, I think the evidence base suggests that trazodone could at least be worth a try, either together with an SSRI, or even on its own.}

Irrational Numbers Metaphor

This is kind of a whimsical post, perhaps you may find it of very questionable relevance to a psychiatry blog.

I invite some input from any number theory experts out there, perhaps some of my thinking about the following subject is erroneous.

Irrational numbers are numbers which cannot be expressed as a ratio of integers. So, for example, the square root of 2 is irrational (it is approximately, but not exactly 1.414; it can be visualized as the distance diagonally across a square which has each side of length=1). The number pi (the ratio of a circle's circumference to its diameter) is irrational, approximately 3.14. The natural exponential base e is irrational, approximately 2.7. If we attempt to express an irrational number in decimal form, we can only ever get an approximation. The digits will keep on going forever, in a non-repeating fashion.

A hypothesis I have about the digit expansion of an irrational number is that the sequence represents a form of true randomness. At one point I did plot out the frequencies of digits in an expansion of pi to a million digits or so, then performed some statistical tests on this, and determined that the results are consistent with random ordering. They MUST be "random", for if they weren't, the number could not be irrational. I would invite a number theorist to show me a proof of this. My idea about randomness invites a philosophical, or mathematical, discussion, about what the meaning of true randomness really is.

But the digits of irrational numbers are calculable. That is, the millionth, or trillionth, digit, in the decimal expansion of pi, can be determined, systematically, through various algorithms. The number e can be calculated in a number of ways (this is a way I discovered as a child, playing with my calculator: take (1+1/n) multiplied by itself n times, with the calculation becoming more and more accurate as n grows larger--only perfectly accurate, though, when n reaches infinity).

So, I am claiming that the digits are calculable, yet randomly ordered. This is a seeming contradiction.

However, I believe there is no simple formula for the "nth" digit of pi. In order to get the "nth" digit, at least n arithmetic steps must be taken. That is, computational work must be done in order to do the calculation, and more computational work is required in order to reach a more precise result, which is at least linearly proportional to the level of precision desired.

Since all computational work requires energy, and there is a finite amount of energy available in the universe, let us suppose that we use all the mass-energy of the universe to perform computational work to determine as many digits of pi, for example, as is possible. (this would involve, in our thought experiment, harnessing all of the great nuclear energies from the stars, etc. to power a computational device just for this task)

Now, having generated all of these digits (I suspect there would be over 10^1000 digits generated, using all the energy of the universe efficiently for this task), we still only have an approximation to the number pi. The NEXT digits of pi are theoretically calculable, but cannot be calculated or known, because we have used all available computational energy.

Thus, we have calculable digits, which yet cannot be known, because there is not enough energy in the universe to do the calculations to know them.

There is something almost mystical about this: any sequence of digits, for example, randomly conceived in the mind, must correspond to a sequence of digits in the unknowable expansion of pi (in that realm over 10^1000 digits into the expansion), based on the laws of probability.

Something that we can prove is outside the realm of human knowledge is actually part of the ordinary daily products of our imagination.

As an added concept related to this, imagine what your entire life history would look like, translated into a sequence of digits -- perhaps this would include a few thousand pages of text, a few million images, together with the entire sequence of your genome, all transformed into a digit sequence, maybe a few trillion digits long.

It can be shown that this sequence -- an intimate representation of your identity -- must occur at some point in the decimal expansion of all irrational numbers, including pi. (suppose the sequence representing your life story is 10 trillion digits long; then the probability of your sequence occurring starting at or before the nth position in pi's expansion is 1-(1-1/(10 trillion))^n, assuming that pi's digit expansion behaves as a random sequence. With this assumption, once you are into pi's expansion by 10 trillion digits, there's a 63% chance that your sequence will have shown up (interestingly, this probability is approximately 1-1/e). And the more digits you go into pi's expansion, the more likely it is that "your" sequence will show up; this probability converges towards 100% as the number of digits approaches infinity. Actually, we could go on to say that "your" sequence actually recurs, an infinite number of times, in pi's expansion!

In our imagination, we can conceive an ideal circle, and we can imagine the ratio between its circumference and its diameter. That is pi exactly. We have imaginatively visualized something, with perfect precision, something that cannot be expressed logically with perfect precision.

There is a life lesson in this, I think. Be open to possibility. That which is seemingly impossible may require an imaginative re-framing to see that it was always in front of you, available to you, part of "ordinary" daily life. And there can be more to simple relationships than meets the eye -- dividing a circumference by a diameter yields a number which contains information paralleling all known information in the universe, including the story of yourself.